|By Gale Staff|
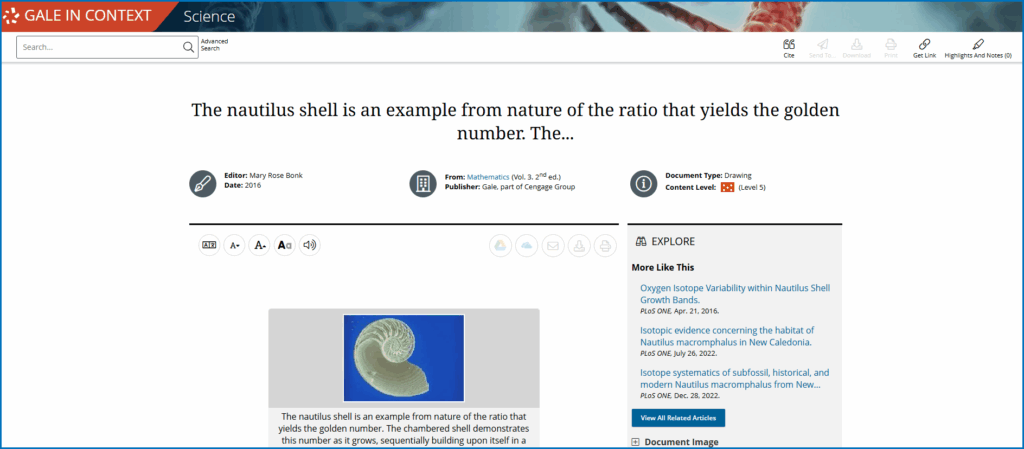
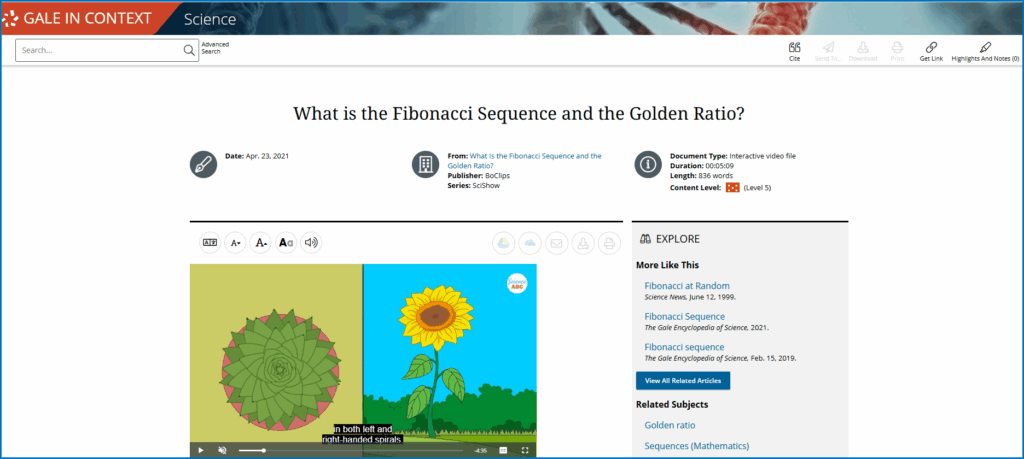
Look at a sunflower, and you’ll see spirals of seeds packed so precisely they seem engineered. The same swirl appears again and again in nature, across the patterns in pine cones and pineapples. From the delicate spiral of a nautilus shell to the storm-borne swirl of a hurricane seen from space and even the twisting arms of distant galaxies—they all share one of nature’s most striking designs: the Fibonacci sequence.
This sequence begins with 1 and 1, and each new number is formed by adding the two before it: 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, and so on.
That’s why November 23—written as 11/23—is celebrated as Fibonacci Day, because the date itself mirrors the beginning of the sequence. It’s a day to recognize how these patterns appear across nature.
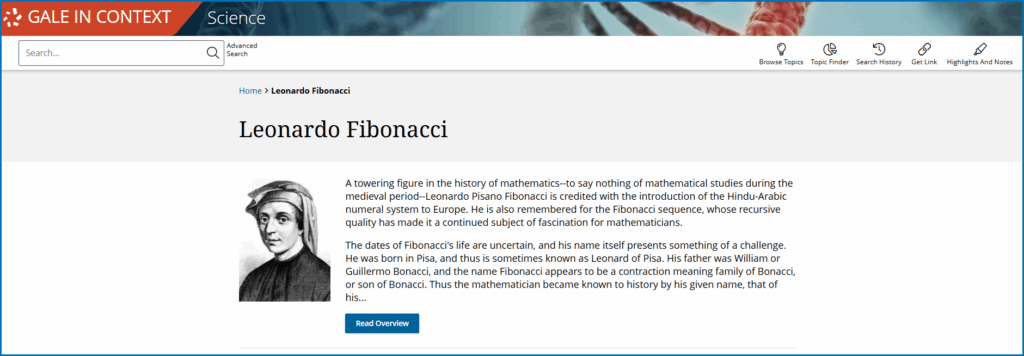
Educators can spark curiosity about this intriguing sequence and support students in pursuing deeper inquiry with Gale In Context: Science. This richly resourced database provides biographies, scholarly articles, and multimedia to illuminate Fibonacci’s life (c. 1170–1250) and the impact of his ideas across design, mathematics, and science.
To celebrate the story of this mathematician from Pisa and why his famous sequence still matters today, you will find links throughout to Gale In Context: Science, making it easy for busy teachers to preview and integrate trustworthy materials into their lessons.
The Life and Learning of Leonardo Bonacci
Pisa around 1170 was a maritime crossroads, with ships and merchants carrying not only goods in and out of port, but also new ideas and innovations. It was into this setting that Leonardo Bonacci, later known simply as Fibonacci (“son of Bonacci”), was born.
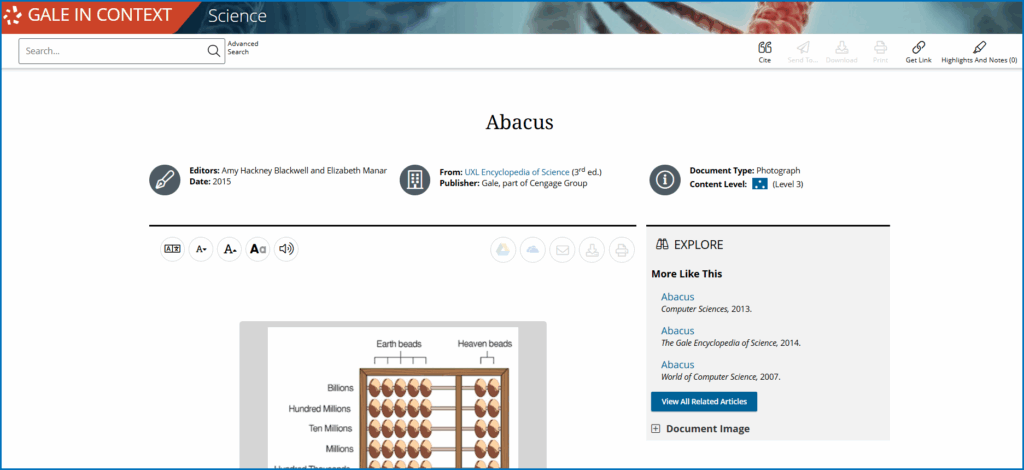
In most medieval European towns, including Pisa, calculations were performed on counting boards and abaci. Clerks slid counters along lined grooves for ones, tens, and hundreds, and “carried” by exchanging ten counters on one line for a single counter on the next.
When the transaction was completed, the user would reset the counters, and only the final answer—often written in words or Roman numerals—would be recorded in the ledger.
Hindu-Arabic Numerals
Fibonacci’s father, Guglielmo, was a merchant who managed Pisan trading interests in North Africa. As a teenager, Leonardo joined him in Bugia, or modern-day Béjaïa, Algeria. Here, young Fibonacci worked under teachers who introduced him to the Hindu-Arabic numeral system.
One notable difference from the European numeration systems was the Hindu-Arabic system’s use of zero as a written placeholder. The idea that “nothing in the tens place” should be written down with its own symbol didn’t exist in European practice, where merchants left such places blank on counting boards.
In Bugia, Fibonacci saw his teachers using digits 0–9 arranged in columns, so that a digit’s place gave it its value. For example, if there were no hundreds, they inserted a 0 to hold the place that would otherwise be left blank.
Without that zero, a clerk might copy 3 47 as 347 instead of 3,047, and even a simple sum like 3,047 + 25 can go wrong if the columns aren’t aligned. The written zero fixes the structure so the meaning of a number survives copying and calculation. With positional writing, the structure of a number is visible on the page, providing the necessary context so that anyone reading the page later can reconstruct its meaning. This mathematical concept is now the bedrock of everything from decimals to scientific notation.
Compared with the more ephemeral nature of counting-board arithmetic, Fibonacci became fascinated by mathematics that he could carry on the page. His curiosity grew as he moved from Algeria to ports in Egypt, Syria, Sicily, and Provence. Along the way, merchants, surveyors, and scholars showed him how written mathematics settled exchange rates, divided profits by capital and time, measured land and timber, and organized astronomical tables.
The Liber Abaci
When Fibonacci returned to Pisa, he shaped what he had learned into a Latin manual, Liber Abaci (1202).
The book teaches readers how to compute with Hindu-Arabic numerals and how to present a solution so that someone else can follow it: name the givens, establish the relationship, carry out the steps, and verify the result.
By writing in this way, Fibonacci helped establish the kinds of everyday business calculations that later Italian abbaco schools would teach—figuring currency exchange, dividing profits, calculating interest, and making measurements. While he covered many different topics in Liber Abaci, two of the most important were rhetorical algebra and proportional reasoning.
Rhetorical Algebra
When Fibonacci studied with teachers in Bugia, he encountered algebra in a format that would seem totally foreign to most mathematicians today: Each step was written in prose.
At this point, equations were not written using the symbols (=, +, -, x, ÷) familiar to us today. Instead, the Arabic-speaking scholarly world drew from earlier Greek and Indian work.
A typical problem might read: Find a number which, when a fifth of itself is added, becomes 21.
The teacher would first have students restate the relation in their own words—the number together with its fifth equals 21—and then solve. Students might choose an easy trial value, like 5, add its fifth (1) to get 6, notice that six must be enlarged to reach 21, and scale the five by the same factor. The result, 17½, satisfies the conditions.
Seen this way, the difference between then and now comes down to notation. Today, we might write x + 1/5x = 21 and solve it in symbols. Fibonacci’s teachers wrote the same structure in words. In both cases, the work begins by naming the quantities and their relationship and then justifying the steps that lead to the answer.
Proportion and the Rule of Three
One of the informal classrooms where Fibonacci learned new ways to think about mathematics was the counting house—a merchant’s office often attached to a warehouse or customs house at a port. Here, clerks handled conversions among currencies, weights, and measures by reasoning in proportion. They began with a known relationship—such as an exchange rate posted at the harbor—and treated that relationship as the basis with which to scale.
This practice was known as the rule of three: three quantities are known, and the fourth is the one that maintains the relationship.
Example: Five lire buys seven bezants. A shipment is priced in bezants. What should eighteen bezants cost in lire?
Here, the three known quantities are:
- 5 lire
- 7 bezants
- 18 bezants
- The unknown quantity is the number of lire equivalent to 18 bezants.
In Fibonacci’s time, merchant ledgers were treated as legal evidence, and a merchant’s reputation depended on recording accurate, mistake-free figures. To avoid errors, merchants used abbaco arithmetic, or testing trial numbers, before completing their full calculations. This method helped them narrow the range of possible correct answers and catch unreasonable results early.
In relation to the above example, a clerk might first note that 18 is a little more than twice 7—so the lire amount should be a bit more than twice 5. Once the final computation produced twelve and six-sevenths lire, it confirmed that the math fell within the expected range and was safe to commit to ink.
The Fibonacci Sequence
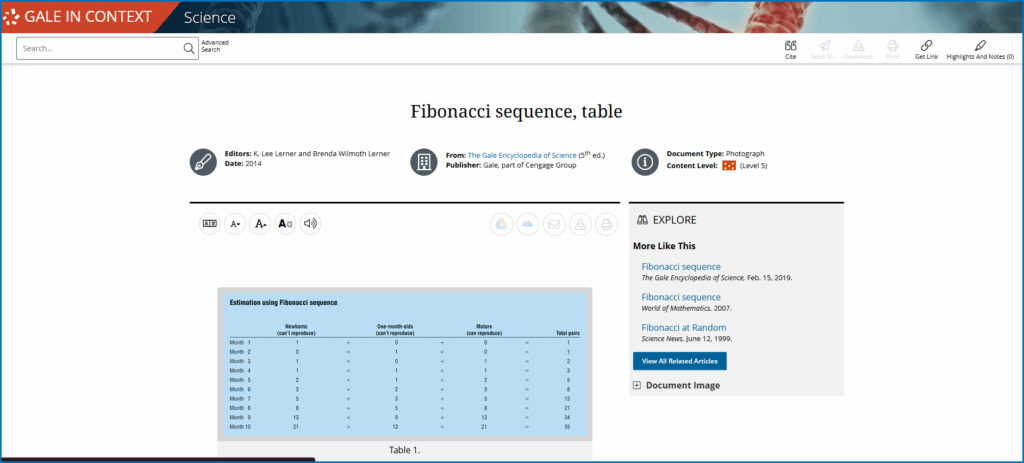
Long before Fibonacci, Indian scholars employed a simple counting method that yields the same numbers we now refer to as the Fibonacci sequence. These ideas expanded out of India and into the Islamic world through medieval mathematicians such as al-Khwarizmi and Abu Kamil.
Fibonacci’s contribution was to popularize the sequence in Europe by publishing it in the Liber Abaci alongside calculation methods through an example involving the breeding of rabbits. That example gave rise to the sequence now named after him.
Why It Still Matters
Fibonacci gives students a first example of a recursive function, or a series of numbers that refers back to its previous terms to generate the next value.
One of the most remarkable outcomes of the Fibonacci sequence is its link to the golden ratio, a constant denoted with φ (phi) and equal to approximately 1.618. If students divide each Fibonacci number by the one before it—2 ÷ 1, 3 ÷ 2, 5 ÷ 3, 8 ÷ 5—the results move closer and closer to that constant.
This ratio defines a concept called the golden rectangle. The proportion between the short and long sides is the same as the proportion between the long sides and the entire shape. Cut a square from it, and the smaller rectangle left behind keeps the same proportions.
This self-repeating balance has captivated artists and architects for centuries because it feels particularly pleasing to the human eye. Artists and architects have used it in their work for centuries, from the Parthenon in Athens to Dalí’s Sacrament of the Last Supper. Even modern design references it—the National Geographic logo is a perfect golden rectangle.
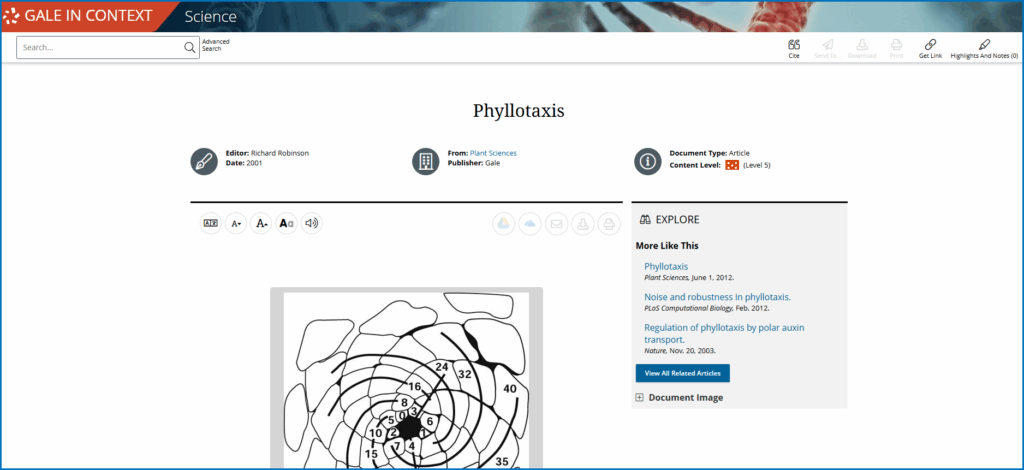
Naturalists have noted the same proportion in snail shells and honeybee populations, but it’s particularly common in plants. Many demonstrate a phenomenon known as phyllotaxis, which refers to the arrangement of leaves, seeds, petals, etc.—the same pattern seen in sunflower heads and pine cones.
Many plants add new elements around a center at a nearly constant divergence angle, so each new piece lands where it gets space and light, at nearly the same angle from the previous one.
When that angle is close to the golden angle of approximately 137.5°, each new piece lands in the least crowded spot, filling in evenly with no long gaps or straight lines. As the structure grows, you can trace families of nearest-neighbor spirals on the surface, and the counts of those spirals most commonly come in adjacent Fibonacci numbers like 34 and 55. Sunflowers, for example, frequently exhibit a ratio of 34/55 or 55/89. Pine cones and pineapples often show 8/13.
Try It in the Classroom: Patterns in Nature
Tie Fibonacci Day to hands-on inquiry with an activity from Gale In Context: Science. This experiment guides students through the process of growing twining plants, varying the light, and observing spiral or helical growth. The project bundles background concepts, procedures, materials, discussion questions, and more, so you can connect the Fibonacci sequence to real observations with minimal prep.
Turn Curiosity Into Curriculum with Gale In Context: Science
Leonardo Fibonacci’s story shows how one life can bridge worlds, connecting concepts like mathematics, commerce, natural phenomena, and fine art.
Gale In Context: Science makes pulling together all of those pieces easier for busy teachers. Within one platform, you can pair a concise biography with clear explanations of sequences and limits, pull in articles on Indian prosody and the Islamic algebraic tradition for origins, and then pivot to classroom-ready pieces on measurement, modeling, and patterns in nature.
Eager to explore Gale In Context: Science for your school or district? Set up a preview for Fibonacci Day—contact your Gale sales representative to learn more about access options and support for educators.